Lorsque vous obtenez 0/0 dans le calcul de la limite d'une fonction racine carrée du type, par exemple, [(x+2)^0,5 / (x-2)],
vous devez utiliser un artifice de calcul pour lever l'indétermination et résoudre ainsi la limite (voir tableau récapitulatif des différentes techniques de résolution des cas indéterminés) en multipliant le dénominateur et le numérateur par le binôme conjugué.
Formule à connaître
Les identités remarquables suivantes doivent être maitrisées.
(A - B) . (A + B) = A2 - B2
On dit que (A - B) est le binôme conjugué de (A + B)
(A2  AB + B2) . (A
AB + B2) . (A 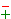 B) = A3
B) = A3  B3
B3
On dit que (A2  AB + B2) est le trinôme conjugué de (A
AB + B2) est le trinôme conjugué de (A  B)
B)
(A  B)2 = A2
B)2 = A2  2AB + B2
2AB + B2
Exemple
Soit la fonction f(x) suivante,
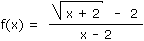
On vous demande de calculer la limite de cette fonction
pour x tendant vers 2.
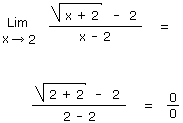
Il s'agit d'un cas indéterminé que nous allons résoudre en multipliant le dénominateur et le numérateur par le binôme conjugué de la façon suivante :
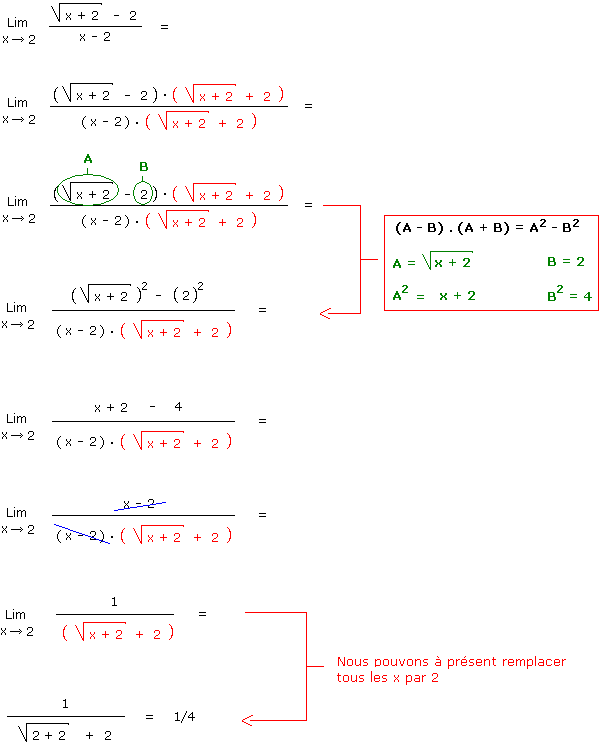
Observez le graphique de la fonction f(x) suivant :
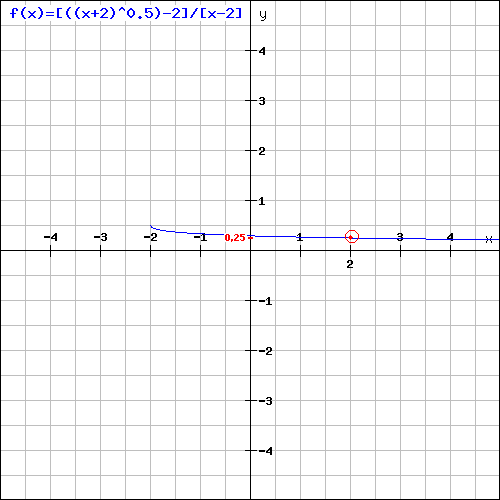
Ce graphique a été tracé à l'aide de notre calculatrice gratuite en ligne.
Vous constatez que la limite de f(x) pour x tendant vers 2 est égale à f(2).
f(2) = 0,25 = 1/4.