Comment calculer la limite d'une fonction en mathématiques ?
Comment résoudre les formes indéterminées en levant l'indétermination via des artifices de calcul ?
Apprenez à utiliser la règle de l'hospital, la factorisation du terme du plus haut degré,...
Découvrez le comportement d'une fonction à l'infini grâce au calcul des limites.
C'est quoi une forme indéterminée ?
Bien souvent en math, lors du calcul d'une limite, vous obtiendrez comme résultat l'une des 7 formes indéterminées
ci-dessus. Une telle solution n'est pas satisfaisante car elle en cache une autre. Pour découvrir la solution "cachée", il faudra utiliser un artifice de calcul pour lever l'indétermination et aboutir
à un résultat final qui sera soit un nombre réel, soit zéro, soit plus l'infini (+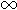 ), soit moins l'infini (-
), soit moins l'infini (-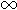 ).
).
Il y a 7 cas d'indétermination dans le calcul des limites.

Les cas indéterminés sont: zéro divisé par zéro, infini divisé par infini, zéro multiplié par infini, infini moins infini,
zéro exposant zéro, infini exposant zéro et un exposant infini.
Opérations mathématiques avec zéro et l'infini
k est une constante réelle non nulle et positive. En langage symbolique on écrit :

Rappel d'algèbre
Identités remarquables, racine carrée et racine cubique, règle d'Horner, factorisation de polynômes, valeur absolue :
(A - B) . (A + B) = A2 - B2
On dit que (A - B) est le binôme conjugué de (A + B)
(A2  AB + B2) . (A
AB + B2) . (A 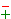 B) = A3
B) = A3  B3
B3
On dit que (A2  AB + B2) est le trinôme conjugué de (A
AB + B2) est le trinôme conjugué de (A  B)
B)
(A  B)2 = A2
B)2 = A2  2AB + B2
2AB + B2
(A  B)3 = A3
B)3 = A3  3A2B + 3AB2
3A2B + 3AB2  B3
B3
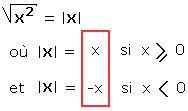
La valeur absolue de x, 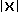 , renvoie toujours un résultat positif.
, renvoie toujours un résultat positif.
Et ce quel que soit le signe de x.
Exemple :

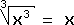 ,
,
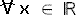
(= x pour tout x appartenant à l'ensemble des nombres réels).
Règle d'Horner :
Factorisation et division de polynômes.
Equation du second degré :
Factoriser une équation du second degré et trouver ses racines x1 et x2 par la méthode du Delta, Δ (discriminant).