Limite de fonction : Lever l'indétermination

Comment résoudre une forme indéterminée ? Nous vous proposons un récapitulatif de tous les cas de figure dans lesquels vous pourrez vous trouver. Vous apprendrez à identifier le type de limite auquel vous avez affaire et à y appliquer une technique de résolution propre à chaque cas afin de lever l'indétermination.

Comment calculer une limite : La règle de base

Soit la fonction f(x) et le calcul de sa limite pour x tendant vers a

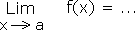
Il faut toujours commencer le calcul d'une limite par remplacer x par la valeur a.

Exemple :

Soit la fonction suivante f(x) = 3x² + x + 1, on vous demande de calculer la limite de la fonction f pour x tendant vers 2 :

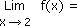
= f(2)
= 3(2)² + 2 + 1
= 12 + 2 + 1
= 15

Forme indéterminée ?

Que faire si après avoir appliqué la règle de base ci-dessus vous obtenez une forme indéterminée ? Pour lever l'indétermination, vous devrez appliquer l'une des régles répertoriées dans le tableau ci-dessous. La règle que vous choisirez d'appliquer dépendra de la forme indéterminée que vous aurez obtenue.

	f(x) = g(x) / h(x)	x est contenu dans une racine	Équation trigonométrique
0/0	- Factoriser ou - Règle de l'Hospital (ou Hôpital) (Factorisation par division de polynome, par horner, ou par identité remarquable)	- Multiplier numérateur et dénominateur par le binôme ou trinôme conjugué ou - Règle de l'Hôpital	Ramener à la forme 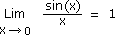Exemples et formules
	- Mettre le terme du plus haut degré en facteur ou - Règle de l'Hospital (ou Hôpital)	- Mettre le terme du plus haut degré en facteur et le sortir de la racine, ou - Règle de l'Hospital (ou Hôpital)	/
	- Mettre le terme du plus haut degré en facteur ou - Ramener au même dénominateur	Multiplier numérateur et dénominateur par le binôme ou trinôme conjugué	/
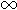
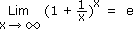
1	Ramener à la forme Exemples et formules (e = 2,718..., c'est la constante de Néper ou nombre exponentiel)	/	/

Ce tableau est un tableau à double entrée. La première colonne du tableau reprend les différents cas d'indéterminations possibles. Tandis que les trois colonnes suivantes reprennent les différents types d'équations possibles (équation avec quotient, racine, et équations trigonométriques).

Comment utiliser ce tableau ? Exemple :

Soit la fonction f(x) = (x² - 4) / (x - 2), on vous demande de calculer la limite de f(x) pour x tendant vers 2.

Pour résoudre cette limite nous allons d'abord remplacer x par 2 dans la fonction f(x) pour voir si nous obtenons un nombre réel, l'infini ou une forme indéterminée. Si le résultat obtenu est un nombre réel, + l'infini ou - l'infini, le calcul s'arrête là. Nous avons notre réponse final. Par contre si le résultat obtenu est une forme indéterminée, nous utiliserons le tableau ci-dessus pour lever l'indétermination.

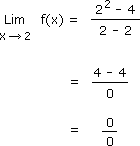
Il s'agit d'une forme indéterminée. Nous devons donc utiliser le tableau ci-dessus.

Comment entrer dans le tableau ?

Premièrement, de quel type de fonction s'agit-il ? S'agit-il d'un quotient f(x)/g(x), d'une racine, ou d'une fonction trigonométrique ?
-> QUOTIENT f(x)/g(x).

Deuxièmement, de quel cas d'indétermination s'agit-il ? S'agit-il de la forme indéterminée 0/0, infini/infini, infini - infini ou 1 exposant infini ?
-> 0/0.

Par conséquent, nous rentrons dans le tableu via la première colonne et la première rangée, ce qui détermine la première case du tableau. Et donc pour résoudre cette limite nous devrons soit factoriser soit utiliser la règle de l'Hôpital. Je vous propose de résoudre cet exemple par factorisation. Nous verrons l'Hôpital plus tard.

Factorisons le numérateur x² - 4 :

nous factorisons le numérateur de cette fraction à l'aide des identités remarquables,

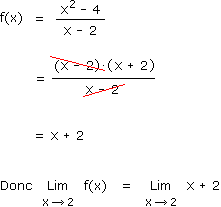
= 2 + 2
= 4

Remarque importante :

Notez que la fonction n'existe pas en x = 2. Donc f(2) n'existe pas. De fait, si vous tracez le graphique de cette fonction a l'aide de la calculatrice graphique en ligne, vous obtiendrez le graphe suivant :

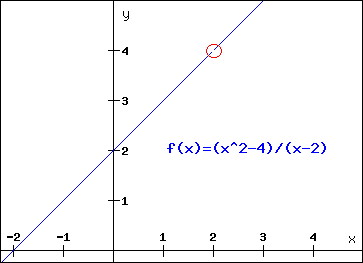
Notez le trou en (2;4). Le point (2;4) n'appartient pas a la droite, la fonction n'est donc pas définie en x = 2. Néanmoins, nous pouvons dire que à mesure que nous nous rapprochons de x = 2, f(x) tend vers 4.