Limites : Règle de l'Hôpital
À quoi sert et comment utiliser la règle de l'Hôpital ? La règle de l'Hospital
permet de lever l'indétermination lors du calcul de la limite d'une fonction lorsque vous obtenez les formes indéterminées suivantes : 0/0 ou infini/infini.
|
|
La Règle de l'Hospital : en 3 étapes
|
Soit f(x) = g(x) / h(x) et nous voulons calculer
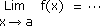
1. Commencez par remplacer tous les x par la valeur a dans la fonction f(x). 2. Si vous obtenez 0/0 ou 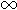 / 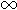alors dérivez le numérateur g(x), puis dérivez le dénominateur h(x) pour obtenir g'(x)/h'(x). Notez que la règle de l'Hospital peut se résumer par la formule suivante :
Maintenant appliquez de nouveau le point 1. en remplaçant tous les x par la valeur a dans g'(x)/h'(x). Si vous obtenez un nombre réel, l'infini ou zéro, vous avez votre réponse, le calcul est terminé. Sinon passez au point 3. ... 3. ... si vous obtenez de nouveau 0/0 ou 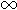/ 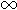alors il faut à nouveau dériver le numérateur et le dénominateur, puis remplacer tous les x par la valeur a, etc.
La règle de l'Hôpital peut s'appliquer plusieurs fois de suite, jusqu'à ce que vous obteniez une réponse différente de 0/0 ou de infini/infini.
|
Exemple :
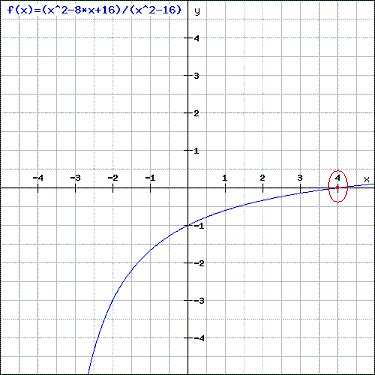
Nous voulons calculer la limite de la fonction f(x) suivante pour x tendant vers 4.
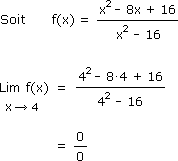
Rappelons que la règle de l'Hôpital ne peut s'appliquer que dans les cas d'indétermination 0/0 ou infini/infini.
Dans notre exemple nous avons la forme indéterminée 0/0, nous appliquons donc l'Hospital.
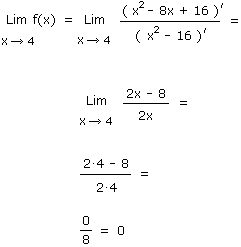
Si vous tracez le graphique de f(x) à l'aide du traceur de fonction en ligne, vous obtenez le graphique suivant :
Vous remarquez que dans notre exemple, le point (4 ; 0) appartient à la courbe. Donc le point (4 ; 0) existe car la fonction f(x) est définie en x = 4. D'où f(4) est égal à la valeur de la limite de f(x) pour x tendant vers 4.
Apprenez également à lever l'indétermination par la mise en facteur du terme du plus haut degré...
