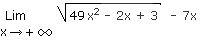Vous trouverez ici des exercices de limite des plus simples aux plus compliqués mais pas seulement !
Nous vous proposons également des exercices plus pratiques où les limites seront appliquées à diverses branches de la science telle que l'économie par exemple.
Limite: exercices corrigés
Accueil > Limites > Exercices résolus - Problèmes résolus
Sommaire
1. Du plus bête au plus méchant
1. Du plus bête au plus méchant
1.1 L'Hôpital 3 fois de suite Solution 1.1
Soit la fonction f(x) suivante
On vous demande de calculer la limite de cette fonction pour x tendant vers l'infini en utilisant la règle de l'Hospital.
1.2 Limite gauche et limite droite Solution 1.2
Soit la fonction f(x) suivante
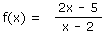
On vous demande de calculer la limite de cette fonction pour x tendant vers 2.
1.3 Lever l'indétermination par factorisation Solution 1.3
Soit la fonction f(x) suivante
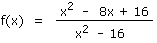
On vous demande de calculer la limite de cette fonction pour x tendant vers 4.
1.4 Multiplier "haut et bas" par les trinômes conjugués Résolution 1.4
On vous demande de calculer la limite suivante :
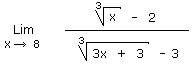
1.5 Calcul de limites et trigonométrie Solution 1.5
Calculez la limite suivante :
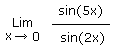
1.6 Infini moins infini sur infini c'est jamais bon ! Solution 1.6
Calculez la limite suivante :
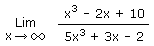
1.7 Sortir un x2 d'une racine comporte un piège Solution 1.7
Calculez la limite suivante :
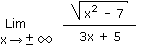
1.8 Le terme du plus haut degré en facteur Solution 1.8
Calculez la limite de la fonction f(x) = 9x2 - 2x + 1
pour x tendant vers +infini ainsi que vers -infini.
1.9 Factoriser une équation du second degré Solution 1.9
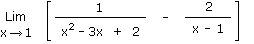
1.10 Multiplication par le binôme conjugué Solution 1.10
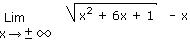
1.11 Le trinôme conjugué encore une fois ! Solution 1.11
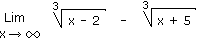
1.12 Limite d'une valeur absolue |x| Solution 1.12
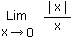
1.13 Déterminer une limite graphiquement Solution 1.13
Soit la fonction suivante
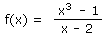
On vous demande d'utiliser notre machine à calculer graphique en ligne pour visualiser cette fonction dans la fenêtre suivante :
Axe des x : de -5 à +5.
Axe des y : de -100 à +100.
Après cela, répondez aux questions suivantes :
a) Déterminez graphiquement la limite de cette fonction pour x s'approchant de 2 par la gauche. Et la même chose lorsque x s'approche de 2 par la droite.
b) Déterminez mathématiquement (par calcul) les valeurs des limites obtenues en a), c'est-à-dire :
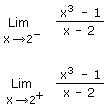
c) La limite pour x -> 2 existe-t-elle ? Si oui, que vaut-elle ? Si non, pourquoi ?
1.14 Limite gauche et limite droite encore une fois ! Solution 1.14
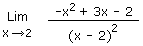
1.15 D'abord factoriser le polynôme par la Règle d'Horner Solution 1.15
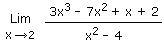
1.16 Résolvez comme d'habitude, ça à l'air juste mais c'est faux ! Solution 1.16
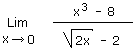
1.17 Utiliser le binôme conjugué puis le trinôme conjugué Solution 1.17
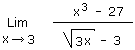
1.18 Comment résoudre ça sans l'Hôpital I ? Solution 1.18
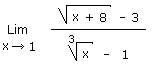
1.19 Comment résoudre ça sans l'Hôpital II ? Solution 1.19
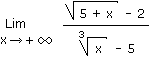
1.20 Infini moins infini comment je fais ? Solution 1.20