Limites - Limite gauche (LG) et limite droite (LD) - Solution de l'exercice 1.2
Allez faire un tour dans notre forum mathématique en ligne... pour discuter de math avec d'autres internautes
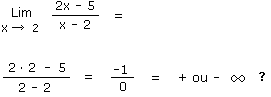
Remarquez qu'il est difficile à ce stade-ci de dire si le résultat sera plus l'infini ou moins l'infini.
Pour résoudre ce problème, nous allons faire un tableau de signe.
Dans notre tableau de signe nous étudions la valeur du numérateur et du dénominateur de f(x) comme suit :

Nous répertorions par ordre croissant, dans le tableau de signe ci-dessus, toutes les valeurs de x qui annulent le numérateur et le dénominateur de f(x) (respectivement x = 2 et x = 5/2). Ce tableau de signe nous permet de constater que le numérateur 2x-5 de f(x) est négatif si x est inférieur à 5/2, nul si x = 5/2 et positif si x est supérieur à 5/2. Tandis que le dénominateur x-2 est négatif si x est inférieur à 2, nul si x = 2 et positif si x est supérieur à 2.
Grâce à ces informations nous pouvons à présent étudier le signe de f(x) puisque f(x) résulte de la division du numérateur par le dénominateur. Nous savons donc maintenant que f(x) est positif si x est inférieur à 2, "impossible" si x = 2, négatif si x est compris entre 2 et 5/2, nul si x = 5/2 et positif si x est supérieur à 5/2.
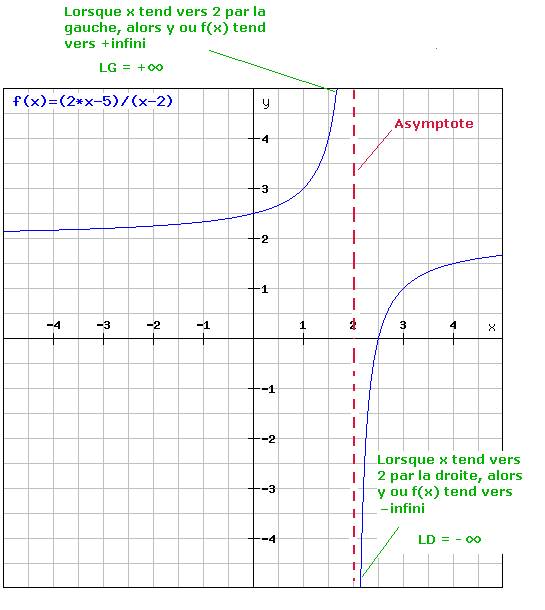
Précisons davantage les choses : en x = 2, la fonction présente une asymptote verticale. A gauche de cette asymptote la courbe monte vers plus l'infini et vient frôler l'asymptote verticale sans jamais la toucher. Cette information nous est donnée dans la dernière rangée du tableau de signe, par le signe "+" a gauche de la barre. Tandis qu'à droite de cette asymptote verticale, la courbe descend vers moins l'infini et vient également frôler l'asymptote verticale sans jamais la toucher. Cette information nous est donnée dans la dernière rangée du tableau de signe, par le signe "-" à droite de la barre.
Nous pouvons d'ailleurs visualiser ce comportement asymptotique en x = 2 à l'aide du graphique de la fonction.
Réponse finale :
Nous pouvons à présent conclure que la limite de la fonction f(x) n'existe pas. Cependant il existe bien une limite gauche (LG) et une limite droite (LD). Ces deux limites s'expriment comme suit :
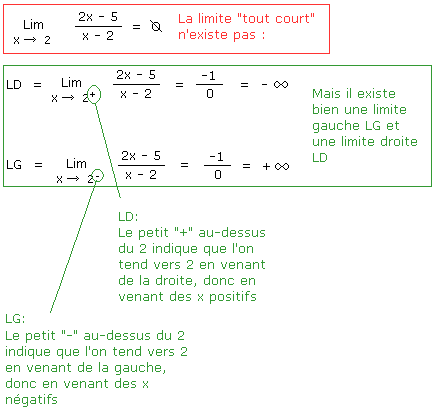
Retenez une chose, nous pourrons dire que la limite "tout court" existe seulement si LD = LG, c'est-à-dire seulement si la limite gauche est égale à la limite droite. Ce qui n'est pas le cas ici.
Quand faudra-il faire un tableau de signe et calculer cette LD et LG ?
Lorsque dans le calcul de la limite suivante,...
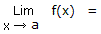
...une mini variation de la valeur de x respectivement au-dessus de a (genre x = a + 0,0001) et en dessous de a (genre x = a - 0,0001) produisent 2 résultats différents lors du calcul de la limite. Un peu d'intuition est nécessaire ici. C'est pourquoi en cas de doute, vous pouvez toujours calculer la LG et la LD à l'aide du tableau de signe. Si vous obtenez LG = LD, alors vous pouvez conclure que la limite "tout court" existe.