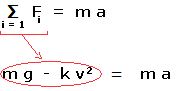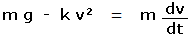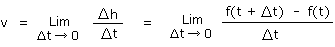Apprenez à mettre en équation un problème réel et pratique nécessitant l'utilisation du calcul de limites. Transformer un problème en équation est beaucoup
plus facile si l'on suit une méthode logique en plusieurs étapes. Voyez vous-même...
Limite: problèmes corrigés
Accueil > Limites > Problèmes résolus
Sommaire
1. Il pleut des parachutes dorés,... c'est la crise ! Solution 1
Hier encore vous étiez numéro 2 de la filiale belge d'une très grosse société américaine. Mais pas de chance pour vous, vous avez été licencié aujourd'hui même suite à la crise économique qui bat son plein depuis l'affaire des subprimes américaines. Anxieux, bien naturellement, les pires craintes envahissent déjà votre esprit. Vos nuits sont hantées par le même cauchemar: vous imaginez les huissiers débarquer dans votre résidence à Lasne pour saisir le Magritte, le Delvaux et le Goya qui hornent respectivement votre salon, cuisine et salle de bain. Ne vous inquiétez pas plus longtemps ! Chacun sait qu'il n'y a généralement pas de crise pour les grands patrons. De fait, comme les autres, vous l'aurez aussi votre parachute doré. C'est ainsi que vous recevez une coquette indemnité de cinq millions d'euros pour vous remercier d'avoir géré avec autant d'imprudence les finances de l'entreprise.
Il est temps maintenant de choisir la banque dans laquelle vous allez placer votre argent. Raisonnable et assagit par la récession économique, vous choisissez de placer (bêtement) votre pactole sur un compte d'épargne. Cependant vous hésitez entre la Deutsche Bank et La Fortis. En effet, les deux banques vous proposent le même taux d'intérêt, à savoir du 6% annuel, néanmoins il subsiste une différence majeure entre les deux offres: la Deutsche Bank vous versera vos intérêts une fois l'an tandis que la Fortis, plus généreuse, vous versera un douzième des intérêts tous les mois.
Vous vous posez alors les questions suivantes :
a). Au bout d'une année, un compte d'épargne de la Deutsche Bank aura-t-il généré autant d'argent, plus d'argent, ou moins d'argent qu'un compte de la Fortis ?
b). Si je place l'entièreté de mes cinq millions d'euros sur mon compte d'épargne, quelle sera la somme obtenue au bout de 5 ans chez Fortis et chez Deutsche Bank ?
c). Quelle serait la somme d'argent accumulée au bout d'un an si la Fortis décidait de vous verser une fraction des intérêts annuels non pas tous les mois ni tous les jours ni même toutes les secondes mais plutôt à chaque instant ! C'est-à-dire que vous disposeriez de vos intérêts de manière instantanée tout au long de l'année. Le capital de départ étant toujours 5000 000 €.
2. Un parachutiste en chute libre, ça tombe vite Solution 2
Avez-vous déjà sauté en parachute ? Non ! Imaginez, demain vous montez dans un avion, celui-ci monte à très haute altitude et vous décidez de sauter. La chute est longue avant l'ouverture de votre parachute. La Terre vous attire avec une accélération de g = 9,81 m/s2. C'est la force de gravité (mg) qui provoque l'accélération de votre corps et donc sa chute. Une accélération de 9,81 m/s2 ça signifie qu'à chaque seconde qui passe, votre vitesse de chute augmente de 9,81 m/s. Au moment où vous sautez votre vitesse est nulle. Après une seconde votre vitesse est de 9,81 m/s. Après deux secondes votre vitesse vaut 19,62 m/s. Après 3 secondes votre vitesse vaudra 29,43 m/s et ainsi de suite.
Répondez aux questions suivantes :
Cette vitesse ne fera-t-elle qu'augmenter ? Si votre chute dure très longtemps atteindrez-vous une vitesse vertigineuse ? N'existe-t-il pas une vitesse limite maximum qu'il est impossible de franchir ? Si cette vitesse maximum existe, que vaut-elle ?
Vous devez vous aider des formules et valeurs suivantes pour répondre aux questions posées ci-dessus.
La loi de Newton dit que la somme des forces appliquées à un corps est égale à la masse de ce corps multiplié par son accélération. Soit
|
Fi représente une des forces appliquée au corps, m est la masse du corps (mg est la force de gravité qui tire le corps vers le bas), a est l'accélération du corps, k est le coefficient de résistance de l'air, v est la vitesse de chute libre du parachutiste (kv2 représente la résistance de l'air). |
Vous savez que tout corps en chute libre dans l'atmosphère subit la résistance de l'air et sa chute est donc ralentie, freinée par l'air. Cette résistance
est fonction de la vitesse de chute élevée au carré : kv2.
Aussi, nous avons vu que la dérivée de la position d'un objet par rapport au temps (dx/dt) donne la vitesse (v) de l'objet. Et bien sachez également que la dérivée de la vitesse par rapport au temps (dv/dt) donne l'accélération (a) de l'objet.
De la loi de Newton découle donc l'équation différentielle suivante :
|
dv/dt est la dérivée de la vitesse par rapport au temps, (dv/dt = a). |
Si les conditions initiales sont v = 0 lorsque t = 0 (c'est-à-dire qu'au moment où le parachutiste saute de l'avion la vitesse de chute est nulle et on enclenche le chronomètre), alors la solution
de cette équation différentielle est :
|
v est la vitesse de chute libre après t secondes, tanh(x) = (ex - e-x) / (ex + e-x) = tangente hyperbolique de x. |
La masse du parachutiste est m = 80 kg.
Le coefficient de résistance de l'air k prendra pour valeur 0,1.
3. Quelle est la relation entre dérivée et limite ? Solution 3
Un hélicoptère survolant la ville de Bruxelles un samedi midi se retrouve dans une situation relativement désagréable : son moteur tombe en panne. A une hauteur de 300 m du sol, les deux pilotes n'ont aucune chance de s'en sortir vivant. L'équation suivante décrit la hauteur (h) qui sépare l'hélicoptère du sol en fonction du temps écoulé (t) durant la chute.
h = -4,9 t2 + 300
a) Trouvez la variation de hauteur Δh si t passe de t = t0 à t = t0 + Δt.
b) Trouvez Δh/Δt et interprétez la signification physique de ce résultat.
c) h est une fonction du temps donc je puis dire que h = f(t). Dans ce cas

Cette équation représente la vitesse moyenne de chute entre l'instant t et t + Δt. De plus
Ce qui représente la vitesse instantanée (v) de l'hélicoptère au temps t.
Nous vous demandons de calculer cette vitesse instantanée de l'hélico au temps t en résolvant la limite proposée ci-dessus.
d) Calculez la dérivée (h') de h par rapport au temps et comparez votre réponse avec celle obtenue dans le calcul de limite en c). Concluez.
e) Calculez la vitesse instantanée (v) de l'hélico en chute libre aux temps t = 0 sec et
t = 7 sec.
4. Archimède, limites, le périmètre du cercle et le nombre Pi Solution 4
Archimède était un grand scientifique Grec né en Sicile à Syracuse vers 287 av. J.-C. et mort à Syracuse en 212 av. J.-C lors du siège de la ville, tué par un soldat Romain.
Il investit beaucoup d'énergie et de temps à rechercher la valeur exacte d'un nombre que nous appelons aujourd'hui Pi (Π).
Nous allons nous baser sur ses travaux ainsi que
sur les travaux de Taylor (1685-1731, Anglais) et de Mac Laurin (1698-1746, Ecossais) pour retrouver la formule du périmètre du cercle :
Périmètrecercle = 2ΠR
R étant le rayon du cercle.
L'idée de base d'Archimède était la suivante : si vous inscrivez un polygone régulier à n côtés dans un cercle et si n tend vers l'infini, alors votre polygone se confond avec le cercle dans lequel il est inscrit.
Nous vous demandons à présent d'utiliser l'idée d'Archimède ainsi que le développement en série de Taylor et de Mac Laurin (voir ci-dessous) pour montrer que la formule du périmètre du cercle est bien périmètre = 2ΠR.
Astuce : Développement en série de Mac Laurin
|
Le développent en série de Mac Laurin nous apprend que le sinus de x peut s'exprimer de la manière suivante : Sin(x) = x - x3/3! + x5/5! - x7/7! + x9/9! - x11/11! + ... Attention, l'unité de l'angle x doit être en radian ! Rappel : Le factoriel de 7 s'écrit 7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040 |