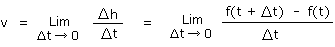Limites et problèmes : Relation entre dérivée et limite ?
Solution du problème 3

Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.

Un hélicoptère survolant la ville de Bruxelles un samedi midi se retrouve dans une situation relativement désagréable : son moteur tombe en panne. A une hauteur de 300 m du sol, les deux pilotes n'ont aucune chance de s'en sortir vivant. L'équation suivante décrit la hauteur (h) qui sépare l'hélicoptère du sol en fonction du temps écoulé (t) durant la chute.

h = -4,9 t² + 300

a) Trouvez la variation de hauteur Δh si t passe de t = t₀ à t = t₀ + Δt.

h₀ = -4,9 t₀² + 300

h₀ + Δh = -4,9 (t₀ + Δt)² + 300

h₀ + Δh = -4,9 ( t₀² + 2t₀Δt + (Δt)² ) + 300

h₀ + Δh = -4,9t₀² - 9,8t₀Δt - 4,9(Δt)² + 300

Δh = -4,9t₀² - 9,8t₀Δt - 4,9(Δt)² + 300 - h₀

Δh = -4,9t₀² - 9,8t₀Δt - 4,9(Δt)² + 300 - (-4,9 t₀² + 300)

Δh = - 9,8t₀Δt - 4,9(Δt)²

Ainsi -9,8t₀Δt - 4,9(Δt)² est la distance chutée durant un intervalle de temps Δt, entre la t₀^ème et la (t₀+Δt)^ème seconde de chute.

b) Trouvez Δh/Δt et interprétez la signification physique de ce résultat.

Δh/Δt = [- 9,8t₀Δt - 4,9(Δt)²] / Δt =

- 9,8t₀ - 4,9Δt

Si vous prenez la route de la mer et que vous roulez 240 km en 2 heures, vous conclurez que vous avez maintenu une vitesse moyenne de 240 km/2h = 120 km/h. Ce qui ne vous a cependant pas empêché de faire des pointes de vitesse à 160 km/h à certains moments ou d'être bloqué dans des embouteillages à du 20 km/h à d'autres moments.

Et bien ici, Δh/Δt représente une distance parcourue divisée par un intervalle de temps : c'est la hauteur chutée durant l'intervalle de temps Δt. Il s'agit donc du calcul d'une vitesse moyenne.

Donc -9,8t₀ - 4,9Δt est l'équation qui donne la vitesse moyenne de chute entre l'instant t₀ secondes et t₀+Δt secondes.

Par exemple, si nous souhaitons connaître la vitesse moyenne entre la 2^ème et la 3^ème seconde de chute il faut prendre t₀ = 2 et Δt = 3 - 2 = 1 sec. D'où

Vitesse moyenne = Δh/Δt = - 9,8 x 2 - 4,9 x 1 = -24,5 m/s

La vitesse moyenne de chute entre la 2^ème et la 3^ème seconde est de -24,5 mètres par seconde. Pourquoi obtenons-nous une valeur négative ? Car l'équation de départ considère qu'un mouvement vertical vers le bas se fait en sens négatif tandis qu'un mouvement vertical vers le haut se ferait en sens positif.

Mais quelle est la vitesse instantanée de l'hélicoptère en chute libre exactement à la deuxième seconde ? Et à la troisième seconde ? La réponse est respectivement 19,6 et 29,4 m/s. Découvrez comment calculer la vitesse inbstantanée plus bas au point e).

c) h est une fonction du temps donc je puis dire que h = f(t). Dans ce cas

Cette équation représente la vitesse moyenne de chute entre l'instant t et t + Δt. De plus

Ce qui représente la vitesse instantanée (v) de l'hélicoptère au temps t puisqu'une vitesse instantanée n'est rien d'autre qu'une vitesse moyenne calculée pour un intervalle de temps très très petit. Or, un intervalle de temps très très petit, c'est un intervalle qui tend vers zéro !

Nous vous demandons de calculer cette vitesse instantanée de l'hélico au temps t en résolvant la limite proposée ci-dessus.

f(t) = -4,9 t² + 300

f(t + Δt) = -4,9 (t + Δt)² + 300

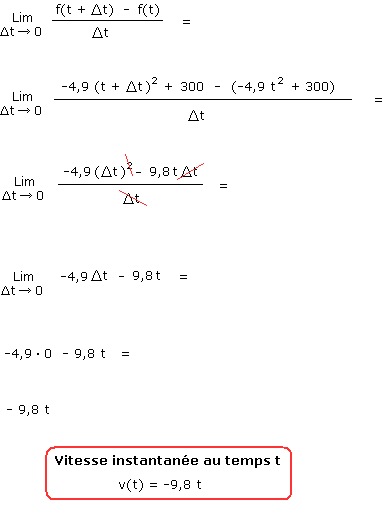
Nous pouvons maintenant calculer la vitesse instantanée de l'hélico en chute à la deuxième seconde par exemple, elle vaut -9,8 x 2 = -19,6 m/s.
Et à la troisième seconde, -9,8 x 3 = -29,4 m/s.

d) Calculez la dérivée (h') de h par rapport au temps et comparez votre réponse avec celle obtenue dans le calcul de limite au point c). Concluez.

Soit h(t) = -4,9 t² + 300,

alors h '(t) = -4,9 x 2 t + 0 = -9,8 t.

Nous constatons que le calcul de la dérivée nous mène à la même réponse que le calcul de la limite au point c).

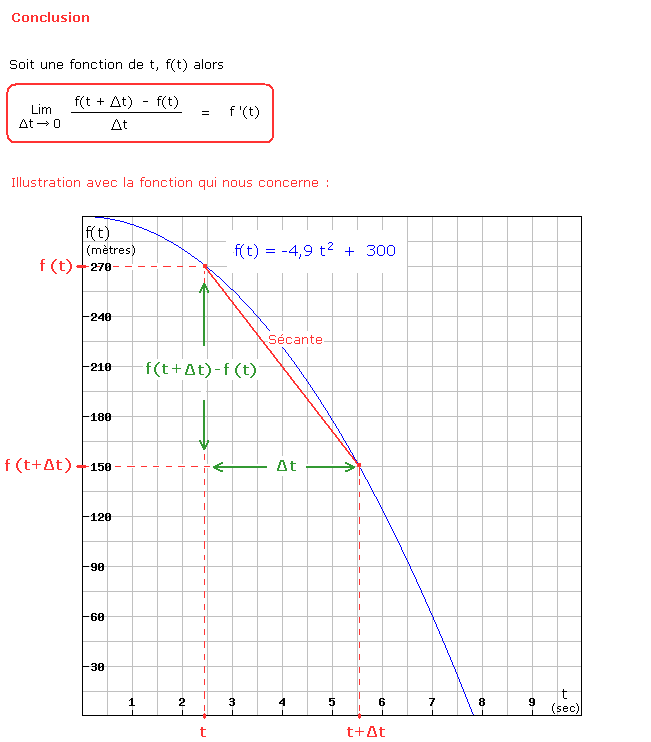
Remarquez que le calcul de la limite proposé ci-dessus n'est autre que le calcul de la pente de la sécante rouge tracée sur le graphique (pour un tout petit intervalle Δt). Or si l'intervalle Δt tend vers zéro, alors la sécante devient tangente à la courbe. Or la pente d'une tangente à la courbe en un point représente la pente de la courbe en ce point. Aussi, on sait que le calcul d'une pente et celui d'une dérivée reviennent au même : une dérivée et une pente c'est pareil !

e) Calculez la vitesse instantanée (v) de l'hélico en chute libre aux temps t = 0 sec et t = 7 sec.

v(0) = -9,8 x 0 = 0 m/s

v(7) = -9,8 x 7 = -68,6 m/s

Remarquez qu'à la 7ème seconde, l'hélicoptère est sur le point de s'écraser au sol avec une vitesse de -68,6 m/s (l'impact se fera un peu avant la 8ème seconde, ça se voit clairement sur le graph ci-dessus). Or -68,6 m/s, cela correspond à une vitesse de -247 km/h. Autant vous dire qu'à cette vitesse, il n'y a aucun espoir pour nos deux pilotes.

Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.