Limites et problèmes : Il pleut des parachutes dorés !
Solution du problème 1

Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.

1. Il pleut des parachutes dorés,... c'est la crise !

Hier encore vous étiez numéro 2 de la filiale belge d'une très grosse société américaine. Mais pas de chance pour vous, vous avez été licencié aujourd'hui même suite à la crise économique qui bat son plein depuis l'affaire des subprimes américaines. Anxieux, bien naturellement, les pires craintes envahissent déjà votre esprit. Vos nuits sont hantées par le même cauchemar: vous imaginez les huissiers débarquer dans votre résidence à Lasne pour saisir le Magritte, le Delvaux et le Goya qui hornent respectivement votre salon, cuisine et salle de bain. Ne vous inquiétez pas plus longtemps ! Chacun sait qu'il n'y a généralement pas de crise pour les grands patrons. De fait, comme les autres, vous l'aurez aussi votre parachute doré. C'est ainsi que vous recevez une coquette indemnité de cinq millions d'euros pour vous remercier d'avoir géré avec autant d'imprudence les finances de l'entreprise.

Il est temps maintenant de choisir la banque dans laquelle vous allez placer votre argent. Raisonnable et assagit par la récession économique, vous choisissez de placer (bêtement) votre pactole sur un compte d'épargne. Cependant vous hésitez entre la Deutsche Bank et La Fortis. En effet, les deux banques vous proposent le même taux d'intérêt, à savoir du 6% annuel, néanmoins il subsiste une différence majeure entre les deux offres: la Deutsche Bank vous versera vos intérêts une fois l'an tandis que la Fortis, plus généreuse, vous versera un douzième des intérêts tous les mois.

Vous vous posez alors les questions suivantes :

a). Au bout d'une année, un compte d'épargne de la Deutsche Bank aura-t-il généré autant d'argent, plus d'argent, ou moins d'argent qu'un compte de la Fortis ?

Deutsche Bank :

Fortis Banque:

Conclusion :

En divisant le taux d'intérêt annuel par 12 et en reversant ainsi sur votre compte un douzième de l'intérêt annuel tous les mois, le mois suivant, l'intérêt est calculé sur un solde plus élevé. C'est ainsi que vous gagnez plus d'argent si vous touchez 12 fois un douzième de 6% que si vous touchez une seule fois par an 6% du capital. La différence est d'ailleurs significative puisqu'à la Fortis Banque vous gagnerez en un an 8389,06 € de plus qu'à la Deutsche Bank.

b). Si je place l'entièreté de mes cinq millions d'euros sur mon compte d'épargne, quelle sera la somme obtenue au bout de 5 ans chez Fortis et chez Deutsche Bank ?

Nous pouvons déduire la formule suivante de la sous question précédente:

Sn = C0 x (1 + r)n Sn est le solde du compte au bout de la nème année. C0 est le capital initial versé sur le compte au départ (5000 000 €). r est le taux d'intérêt annuel exprimé avec un nombre décimal. Exemple: pour un taux d'intérêt annuel de 6% alors r = 6/100 = 0,06. n représente l'année écoulée. Par exemple, au moment ou l'on dépose le capital initial sur le compte en banque, n = 0. Un an plus tard, n = 1. Et lorsque 2 années se seront écoulées après avoir déposé le capital initial sur le compte alors n = 2.

Deutsche Bank :

Au bout de 5 ans le solde accumulé sur le compte en banque sera

S₅ = C₀ x (1 + r)⁵ =

5000 000 x (1 + 6/100)⁵ = 6691127,9 €

J'ai donc gagné 1 691 127,9 € en 5 ans.

Fortis Banque :

Ici la mesure du temps écoulé ne se fera pas en années mais en mois. Par conséquent le n représentera les mois écoulés. Donc 5 années correspondra à 5 x 12 mois = 60 = n. Tandis que le terme r représentera un taux d'intérêt mensuel soit le douzième de 6%.

r = 0,06/12 = 0,005.

Au bout de 5 ans (ou plutôt 60 mois) le solde accumulé sur le compte en banque sera

S₆₀ = 5000 000 x (1 + 0,005)⁶⁰ = 6744250,8 €

J'ai donc gagné 1 744 250,8 € en 5 ans.

Conclusion :

Sur une période de 5 ans, j'ai gagné 53 122,9 € en plus chez Fortis que chez Deutsche Bank.

c). Quelle serait la somme d'argent accumulée au bout d'un an si la Fortis décidait de vous verser une fraction des intérêts annuels non pas tous les mois ni tous les jours ni même toutes les secondes mais plutôt à chaque instant ! C'est-à-dire que vous disposeriez de vos intérêts de manière instantanée tout au long de l'année. Le capital de départ étant toujours 5000 000 €.

Je vous propose d'adapter la formule vue ci-dessus.

Sk = C0 x (1 + r/k)k Sk est le capital total qui se trouve sur votre compte en banque au bout d'une année de placement. r représente le taux d'intérêt fixe annuel en valeur décimale, 0,06 dans notre exercice. k représente le nombre de fois par an que la banque vous verse un kème de vos intérêts (à savoir 5000 000 € x 0,06/k ).

Si vous touchiez vos intérêts toutes les semaines, alors k = 52 (car il y a 52 semaines dans une année). Cela signifie que vous toucheriez un 52^ème de 6% de 5000 000 € soit
(0,06/52) x 5000 000 = 5769,2 € par semaine.

Si vous touchiez vos intérêts tous les jours, alors k = 365 (car il y a 365 jours dans un an). Cela signifie que vous toucheriez un 365^ème de 6% de 5000 000 € soit
(0,06/365) x 5000 000 = 821,9 € par jour.

Si vous touchiez vos intérêts toutes les secondes, alors k = 31536000 (car il y a 31536000 secondes dans une année). Cela signifie que vous toucheriez un 31536000^ème de 6% de 5000 000 € soit (0,06/31536000) x 5000 000 = 0,95 eurocents par seconde.

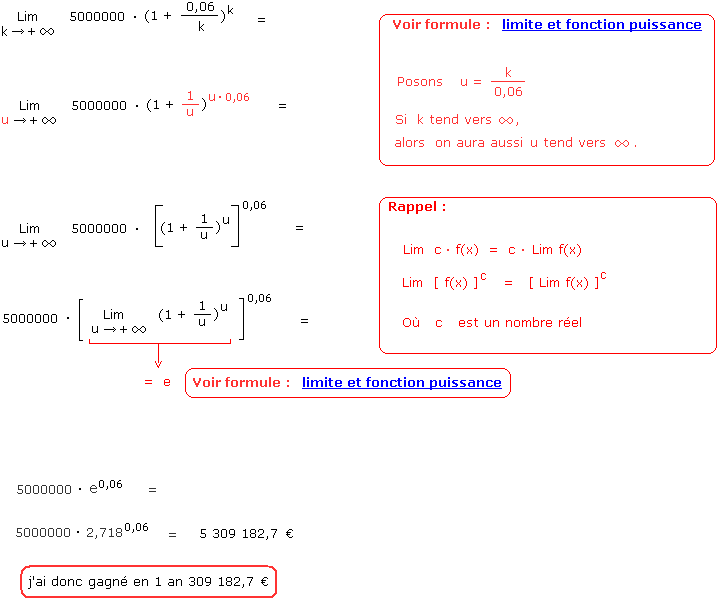
Mais si k = infini alors ça veut dire que vous touchez vos intérêts à chaque instant. Vos intérêts vous sont versés de manière instantanée à mesure que le temps s'écoule. Pour calculer le capital total au bout d'une année, vous devriez alors réaliser le calcul suivant:

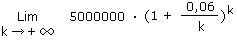
Comment calculer ce genre de limite ? Il s'agit du calcul de la limite d'une fonction puissance (c'est-à-dire avec la variable en exposant). Utilisez la formule vue dans le rappel théorique.

Conclusion :

Lorsque vous placiez votre argent chez Deutsche Bank avec un taux d'intérêt annuel de 6% vous gagniez à la fin de l'année 300 000 €.

Chez Fortis Banque, en touchant un douzième de 6% tous les mois, vous aviez gagné
308 389,06 € après une année de placement.

Et chez Fortis, avec un intérêt calculé en chaque instant et reversé sur votre compte instantanément, vous avez gagné en fin d'année 309 182,7 €.

Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.