Math en ligne > Limites: Th. & Ex. > Forme indéterminée > Lever l'indétermination > Fonction puissance


Calculer la limite d'une fonction puissance

Lorsque vous obtenez 1infini dans le calcul de la limite d'une fonction puissance du type, par exemple, (1 + 1/x)x, vous devez utiliser un artifice de calcul pour lever la forme indéterminée et résoudre la limite (voir tableau récapitulatif des différentes techniques de résolution des cas indéterminés).


Formule à connaître

Comment on fait pour calculer la limite d'une fonction puissance, avec x en exposant

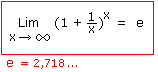
e = 2,718... C'est la constante de Néper ou nombre exponentiel.


Exemple

Soit la fonction f(x) = (1 + 1/2x)x, on vous demande de calculer la limite de cette fonction pour x tendant vers l'infini.

calculer la limite de f(x) = (1 + 1/2x)^x avec x tendant vers l'infini

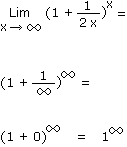
Il s'agit d'une forme indéterminée que nous allons lever par l'artifice de calcul suivant :

Posons u = 2x

Dans ce cas, si x tend vers l'infini alors 2 fois x, et donc u, tendent également vers l'infini.

Nous pouvons donc écrire le calcul suivant :

calculer la limite de la fonction puissance suivante f(x) = (1 + 1/2x)^x avec x en exposant

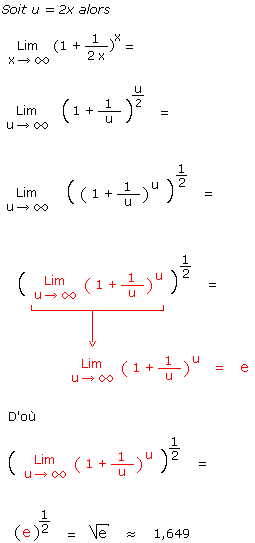
Observez ci-dessous le graphique de la fonction f(x)

tracer le graphique d'une fonction puissance avec x en exposant
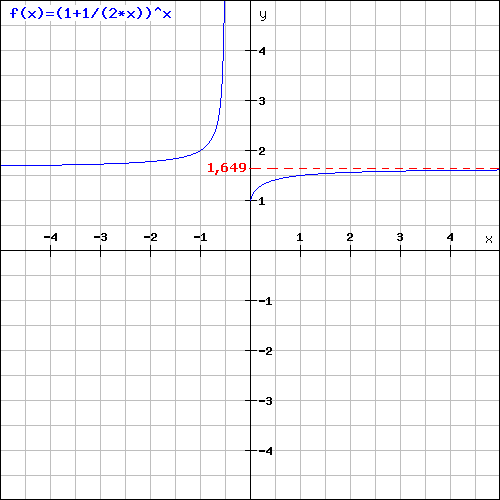
Graphique tracé à l'aide de notre calculatrice scientifique graphique en ligne (utilisation gratuite).

Vous remarquez que pour de grandes valeurs de x (donc pour x tendant vers l'infini), la courbe devient de plus en plus horizontale et tend vers une asymptote horizontale. Cette asymptote horizontale coupe l'axe des ordonnées en y = 1,649, son équation est donc
y = 1,649 (pour info).

Le problème 1 : Il pleut des parachutes dorés,... c'est la crise ! utilise la formule de la limite d'une fonction puissance pour calculer le solde d'un compte dont le taux d'interêt est reversé instantanément (c'est-à-dire en chaque instant au lieu d'une fois par an) sur le compte du client.


Je vous propose à présent d'apprendre à lever l'indétermination en multipliant le dénominateur et le numérateur par le binôme conjugué...

← Limite de fonction                 Multiplier par le binôme conjugué →