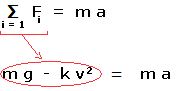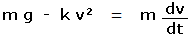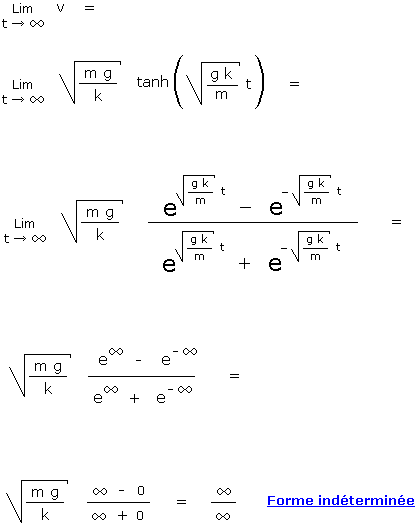Limites et problèmes : Un parachutiste en chute libre
Solution du problème 2

Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.

Avez-vous déjà sauté en parachute ? Non ! Imaginez, demain vous montez dans un avion, celui-ci monte à très haute altitude et vous décidez de sauter. La chute est longue avant l'ouverture de votre parachute. La Terre vous attire avec une accélération de g = 9,81 m/s². C'est la force de gravité (mg) qui provoque l'accélération de votre corps et donc sa chute. Une accélération de 9,81 m/s² ça signifie qu'à chaque seconde qui passe, votre vitesse de chute augmente de 9,81 m/s. Au moment où vous sautez votre vitesse est nulle. Après une seconde votre vitesse est de 9,81 m/s. Après deux secondes votre vitesse vaut 19,62 m/s. Après 3 secondes votre vitesse vaudra 29,43 m/s et ainsi de suite.

Répondez aux questions suivantes :

Cette vitesse ne fera-t-elle qu'augmenter ? Si votre chute dure très longtemps atteindrez-vous une vitesse vertigineuse ? N'existe-t-il pas une vitesse limite maximum qu'il est impossible de franchir ? Si cette vitesse maximum existe, que vaut-elle ?

Vous devez vous aider des formules et valeurs suivantes pour répondre aux questions posées ci-dessus.

La loi de Newton dit que la somme des forces appliquées à un corps est égale à la masse de ce corps multiplié par son accélération. Soit

Fi représente une des forces appliquée au corps, m est la masse du corps (mg est la force de gravité qui tire le corps vers le bas), a est l'accélération du corps, k est le coefficient de résistance de l'air, v est la vitesse de chute libre du parachutiste (kv2 représente la résistance de l'air).

Vous savez que tout corps en chute libre dans l'atmosphère subit la résistance de l'air et sa chute est donc ralentie, freinée par l'air. Cette résistance est fonction de la vitesse de chute élevée au carré : kv².

Aussi, nous avons vu que la dérivée de la position d'un objet par rapport au temps (dx/dt) donne la vitesse (v) de l'objet. Et bien sachez également que la dérivée de la vitesse par rapport au temps (dv/dt) donne l'accélération (a) de l'objet.

De la loi de Newton découle donc l'équation différentielle suivante :

dv/dt est la dérivée de la vitesse par rapport au temps, (dv/dt = a).

Si les conditions initiales sont v = 0 lorsque t = 0 (c'est-à-dire qu'au moment où le parachutiste saute de l'avion la vitesse de chute est nulle et on enclenche le chronomètre), alors la solution de cette équation différentielle est :

v est la vitesse de chute libre après t secondes, tanh(x) = (ex - e-x) / (ex + e-x) = tangente hyperbolique de x.

La masse du parachutiste est m = 80 kg.

Le coefficient de résistance de l'air k prendra pour valeur 0,1.

La solution de cet exercice sera beaucoup plus courte que son énoncé. Pour le résoudre, il suffira de prendre la solution de l'équation différentielle et de calculer la vitesse v atteinte pour un temps de chute t infini. Autrement dit, si vous calculez la limite de la vitesse pour un temps t tendant vers l'infini, vous obtenez la réponse à la question.

Infini divisé par infini est un cas indéterminé qu'il nous faut lever.

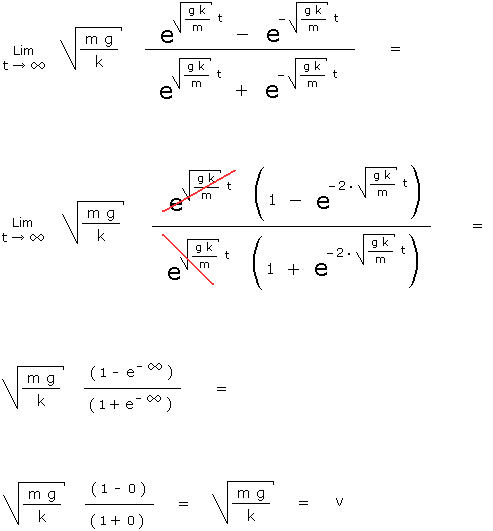
Conclusion :

Si la masse du parachutiste est 80 kg et que la valeur du coefficient de résistance de l'air est k = 0,1, alors la vitesse de chute maximum qu'un corps en chute libre peut atteindre dans l'atmosphère terrestre vaut :

v_max = (mg/k)^1/2 = (80 x 9,81 / 0,1)^1/2 = 88,6 m/s = 318,9 km/h.

Donc si vous pesez 80kg, vous ne dépasserez jamais les 318,9 km/h même si votre chute libre dure un temps infiniment long !

Et sur la Lune ? Qu'en serait-il :

Vous savez que la Lune ne comporte pas d'atmosphère. Cette absence d'atmosphère lunaire à pour conséquence que les sons ne se propagent pas. C'est-à-dire que si vous jetez une grosse pierre sur le sol lunaire, celle-ci s'écrasera à vos pieds dans le silence le plus complet. Et ce silence lunaire absolu ne sera pas non plus perturbé par l'impact d'une météorite par exemple. Mais surtout, qui dit absence d'atmosphère dit absence de résistance de l'air. L'équation différentielle dérivée de la loi de Newton sera donc :

m x dv/dt = m x g_lune

Et la solution de cette équation différentielle est :

v = g_lune x t

Nous savons que la gravité lunaire est six fois moindre que la gravité terrestre :

g_lune = 9,81/6 = 1,63 m/s²

La limite de la vitesse v pour un temps t qui tend vers infini donne un résultat infini. Donc si le temps de chute est infini, la vitesse de chute atteindra également une valeur infinie. Mais ceci n'est vrai qu'en théorie puisqu' aucun corps ne peut dépasser la vitesse de la lumière selon la théorie de la relativité d'Einstein.

Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.