Limites, Archimède, le périmètre du cercle et le nombre Pi
Solution du problème 4
Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.
Archimède était un grand scientifique Grec né en Sicile à Syracuse vers 287 av. J.-C. et mort à Syracuse en 212 av. J.-C lors du siège de la ville, tué par un soldat Romain.
Il investit beaucoup d'énergie et de temps à rechercher la valeur exacte d'un nombre que nous appelons aujourd'hui Pi (Π).
Nous allons nous baser sur ses travaux ainsi que
sur les travaux de Taylor (1685-1731, Anglais) et de Mac Laurin (1698-1746, Ecossais) pour retrouver la formule du périmètre du cercle :
Périmètrecercle = 2ΠR
R étant le rayon du cercle.
L'idée de base d'Archimède était la suivante : si vous inscrivez un polygone régulier à n côtés dans un cercle et si n tend vers l'infini, alors votre polygone se confond avec le cercle dans lequel il est inscrit.
Nous vous demandons à présent d'utiliser l'idée d'Archimède ainsi que le développement en série de Taylor et de Mac Laurin (voir ci-dessous) pour montrer que la formule du périmètre du cercle est bien périmètre = 2ΠR.
Astuce : Développement en série de Mac Laurin
|
Le développent en série de Mac Laurin nous apprend que le sinus de x peut s'exprimer de la manière suivante : Sin(x) = x - x3/3! + x5/5! - x7/7! + x9/9! - x11/11! + ... Attention, l'unité de l'angle x doit être en radian ! Rappel : Le factoriel de 7 s'écrit 7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040 |
Voici un schéma de la situation :
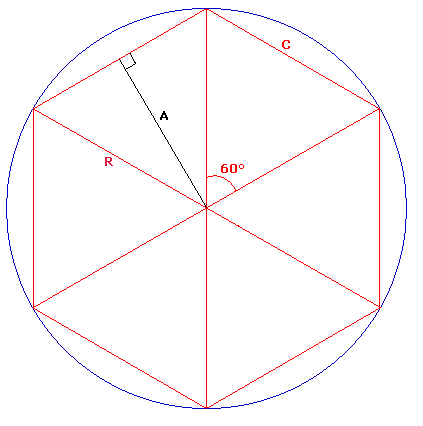
R est le rayon du cercle,
C est la longueur d'un côté du polygone (hexagone) inscrit dans le cercle,
A est l'apothème de l'hexagone, c'est-à-dire la hauteur d'un des 6 triangles qui composent l'hexagone.
L'hexagone divise le cercle en 6 parties égales donc l'angle d'un triangle au centre vaut 360°/6 = 60°. Et l'angle entre l'apothème A et le rayon R vaut 60°/2 = 30° puisque l'apothème A est aussi bissectrice de l'angle.
En utilisant nos connaissances de base en trigonométrie, nous pouvons caluler la longueur du côté C comme suit :
Calculons d'abord C/2,
C/2 = R sin(60°/2) = R sin(30°)
d'où C = 2 R sin(30°)
Or notre hexagone régulier comporte 6 côtés donc son périmètre vaut :
Périmètrehexagone = 6 C = 12 R sin(30°).
Imaginons maintenant que notre polygone inscrit soit un polygone régulier non pas à 6 côtés mais à n côtés. Dans ce cas, le cercle sera divisés en n parts égales et chaque petit triangle aura un angle au centre de 360°/n. Quant à l'angle entre l'apothème A et le rayon R, celui-ci vaudra la moitié de 360°/n, c'est-à-dire 360°/2n.
Réalisons à présent les mêmes calculs que pour l'hexagone afin de calculer le périmètre de notre polygone à n côtés :
Calculons d'abord C/2,
C/2 = R sin(360°/2n) = R sin(180°/n)
d'où C = 2 R sin(180°/n)
Or notre polygone régulier comporte n côtés donc son périmètre vaut :
Périmètrepolygone à n côtés = n C = 2 n R sin(180°/n).
Que se passerait-il si notre polygone comportait une infinité de côtés, c'est-à-dire si n tendait vers l'infini ?
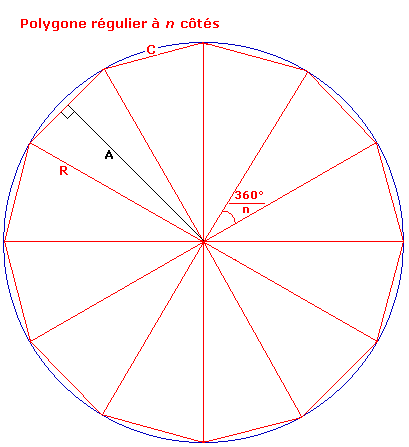
Voyez comme le périmètre du polygone tend à se confondre avec le périmètre du cercle à mesure que le nombre n de côtés augmente. Essayons de caluler le périmètre du polygone régulier dont le nombre de côté tend vers l'infini.
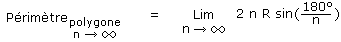
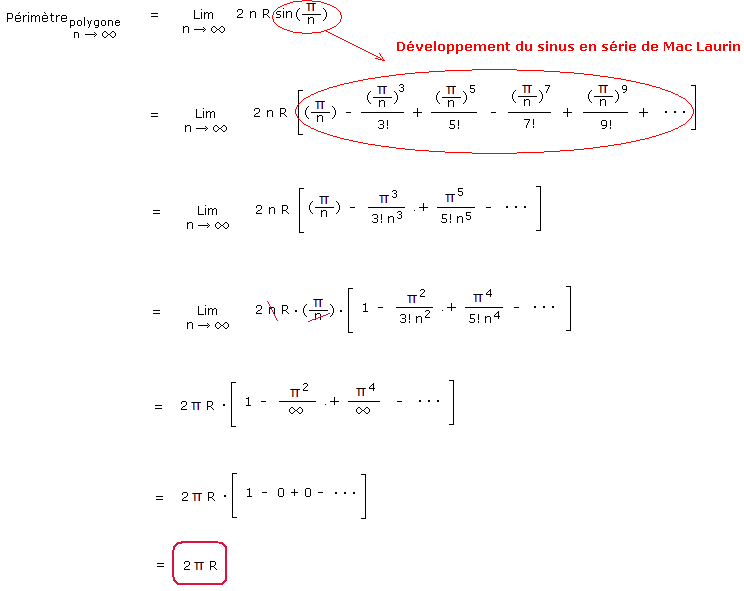
Transformons les 180° en radian afin de pouvoir développer la fonction sinus en série de Mac Laurin. Nous savons que 180° valent Π radians. Remplaçons cela dans le calcul et développons ce sinus avec la formule de Mac Laurin :
Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.