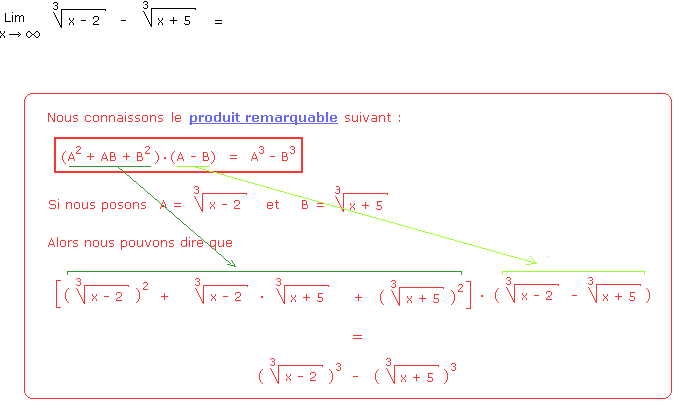
Limites : le trinôme conjugué encore une fois !
Solution de l'exercice 1.11

Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur privé en ligne vous aide en Math ou en Physique! Inscrivez-vous !

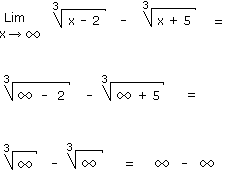
En remplaçant x par infini nous obtenons le cas indéterminé infini-infini. Nous allons lever ce cas d'indétermination en multipliant le numérateur et le dénominateur par le trinôme conjugué comme nous l'avions déja fait dans l'exercice 1.4.

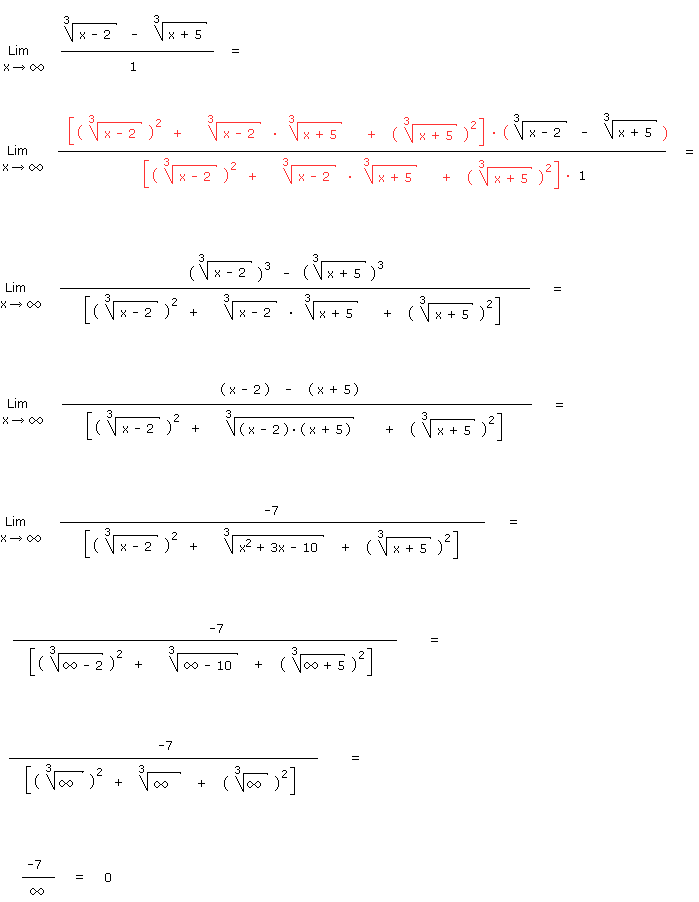
Observons le graphique de la fonction étudiée :

On voit clairement sur ce graphe que lorsque les valeurs de x deviennent très grandes, c'est-à-dire lorsque x tend vers +infini, la courbe se rapproche de l'axe des x pour le longer, pour le frôler, pour s'en rapprocher mais sans jamais l'atteindre. Or sur l'axe des x, la coordonnée y vaut toujours zéro. Et en effet, notre calcul de limite nous montre que la fonction tend vers 0 lorsque x tend vers +infini. Nous venons ainsi de calculer l'équation de l'asymptote horizontale. Cette équation est y = 0.

Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur privé en ligne vous aide en Math ou en Physique! Inscrivez-vous !