Limite gauche et limite droite
Solution de l'exercice 1.13

Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur privé en ligne vous aide en Math ou en Physique! Inscrivez-vous !

Soit la fonction suivante

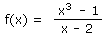
On vous demande d'utiliser notre machine à calculer graphique en ligne pour visualiser cette fonction dans la fenêtre suivante :

Axe des x : de -5 à +5.

Axe des y : de -100 à +100.

Après cela, répondez aux questions suivantes :

a) Déterminez graphiquement la limite de cette fonction pour x s'approchant de 2 par la gauche. Et la même chose lorsque x s'approche de 2 par la droite.

Le graphique montre clairement que si un petit bonhomme se balade le long de la courbe en venant de la gauche, c'est-à-dire des x négatifs, et bien lorsqu'il arrivera à proximité de x = 2, le petit bonhomme sera précipité dans une chute vertigineuse vers le bas (pléonasme,... je sais), c'est-à-dire vers les y négatifs. Nous pouvons donc dire que la limite gauche de la fonction vaut -infini. En langage mathématique ça donne ceci :

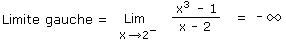
Maintenant si le petit bonhomme décide de se balader le long de la courbe en venant de la droite, c'est-à-dire en venant des x positifs, et bien lorsqu'il arrivera tout près de x = 2, le petit bonhomme s'envolera soudainement vers les cieux, c'est-à-dire vers les y positifs. Nous pouvons donc dire que la limite droite de la fonction vaut +infini. Ceci se traduit en language mathématique par:

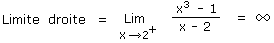
b) Déterminez par calcul les valeurs des limites obtenues en a) :

Soit f(x) = (x³ - 1)/(x - 2), pour calculer la limite de cette fonction lorsque x -> 2 il faut avant toute chose remplacer x par 2. Le problème si vous faite cela, c'est que vous allez obtenir (8 - 1)/(2 - 2) = 7/0 = +infini. Ce qui n'est pas tout à fait juste.

Pour obtenir la réponse correcte et complète, il faut faire un tableau de signe :

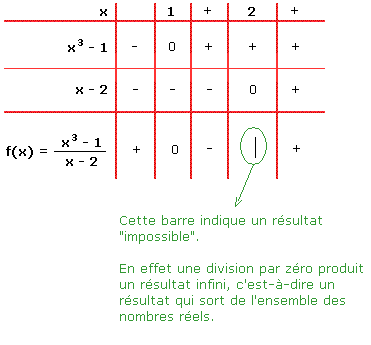
Dans ce tableau de signe, la barre verticale indique une division par zéro, c'est-à-dire un résultat infini. Cependant ce résultat peut être +infini ou -infini. Comment savoir dans quel cas sommes-nous ? Regardez le signe moins à gauche de la barre, cela signifie que la fonction est de signe négatif, le résultat est donc moins infini pour la limite gauche. Même raisonnement pour le signe plus à droite de la barre, nous pouvons donc conclure que la limite droite vaut +infini.

Nous venons de confirmer par calcul les résultats trouvés graphiquement en a).

c) La limite pour x -> 2 existe-t-elle ? Si oui, que vaut-elle ? Si non, pourquoi ?

Non cette limite n'existe pas. Pourquoi ? Parce que si la limite gauche n'est pas égale à la limite droite, alors la limite n'existe pas. Par contre les limites gauches et droites existent et valent respectivement -infini et +infini.

Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur privé en ligne vous aide en Math ou en Physique! Inscrivez-vous !