Limites de fonctions trigonométriques
Solution de l'exercice 1.5

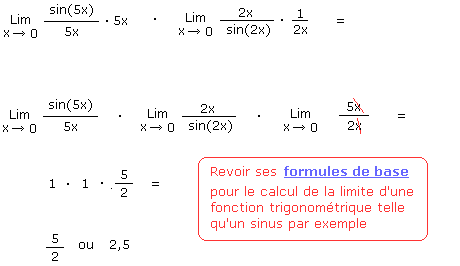
Si vous essayez de résoudre la limite de [sin(5x)] / [sin(2x)] pour x tendant vers 0 directement en remplaçant x par 0 vous obtiendrez la forme indéterminée 0/0. Vous allez donc devoir lever cette forme indéterminée par un artifice de calcul.

Avant d'essayer de lever l'indétermination remmettez-vous en mémoire les formules de base du calcul de limites de fonctions trigonométriques.

Or nous savons que la limite d'un produit est égale au produit des limites :

Lim(a . b) = Lim(a) . Lim(b) d'où

Regardez le graphique de la fonction f(x) = sin(5x) / sin(2x)

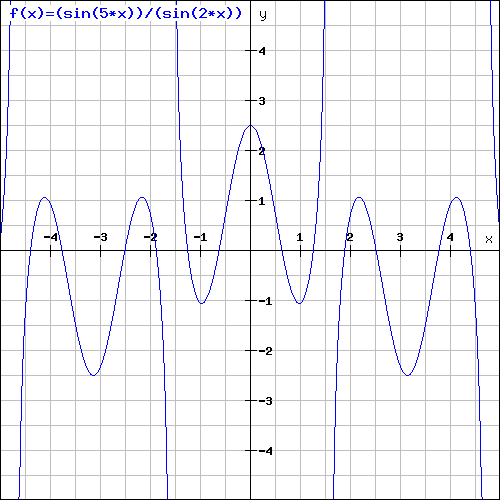
La fonction n'est pas définie pour x = 0. Il n'existe donc pas de point sur la courbe en x = 0. Il y a donc un trou sur la courbe en x = 0. Cependant on voit très clairement que lorsque x tend vers 0, alors y tend vers 2,5.

Ce graphique à été tracé à l'aide de notre calculatrice scientifique et graphique en ligne.

Pour voir un exemple détaillé d'une fonction non définie en un point avec un trou sur la courbe...