Limite : Ca à l'air juste et pourtant c'est faux !
Solution de l'exercice 1.16
Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur de science en ligne vous aide en Math ou en Physique! Inscrivez-vous !
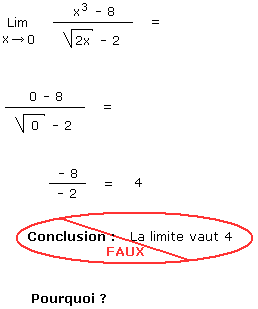
Pour comprendre la raison de cette erreur, je vous propose de d'abord analyser le graphique de la fonction :
Vous constatez que la zone du graphe située à gauche de l'axe des y ne comporte pas de points. Pourquoi ? Car dans cette zone le signe de x est
négatif. Or si x est négatif alors l'argument (le contenu) de la racine carrée au dénominateur de notre fonction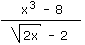 
sera lui aussi négatif. Et je suppose
que vous n'allez pas sans savoir que l'argument d'une racine paire ne peut jamais être négatif. D'ailleurs la raison en est très simple: allez me calculer la racine carrée de -4,
j'aime autant vous dire que vous pouvez chercher la vie entière, vous ne trouverez jamais un nombre qui multiplié par lui même donne -4 !
Et alors quoi ? Et bien la limite pour x tend vers 0 par la gauche (voir explications sur la limite gauche, LG) n'existe pas puisque il n'existe pas de courbe à gauche de x = 0. En effet x ne peut pas être égale à -0,00001, donc x ne peut pas tendre vers 0 par la gauche, donc LG inexistante.
Cependant x peut tendre vers 0 par la droite puisque x peut valoir 0,00001 donc la limite droite (LD) existe. Et cette limite vaut 4.
LG n'existe pas tandis que LD = 4. |
Remarque :
vous n'avez pas le droit d'utiliser une calculatrice graphique en classe ? Peu importe, faites un tableau de signe pour étayer votre argumentation en
hachurant la partie du tableau qui se trouve à gauche de x = 0. Ou plus simplement étayez en précisant que le domaine de définition de votre fonction est [0 ; 2[ U ]2 ; infini[ et ensuite balancez le blabla ci-dessus.
Remarquez que x = 2 n'appartient pas au domaine de définition de la fonction, c'est d'ailleurs pour cela que l'on observe un trou dans la courbe à cet endroit.
Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur de science en ligne vous aide en Math ou en Physique! Inscrivez-vous !