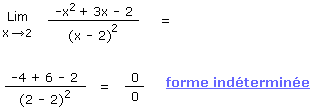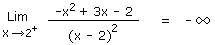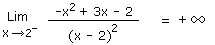Limite : Trouvez la limite de f(x) = (-x2 + 3x - 2)/(x - 2)2
Solution de l'exercice 1.14
Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur privé en ligne vous aide en Math ou en Physique! Inscrivez-vous !
Comment lever cette indétermination ? Par factorisation du numérateur !
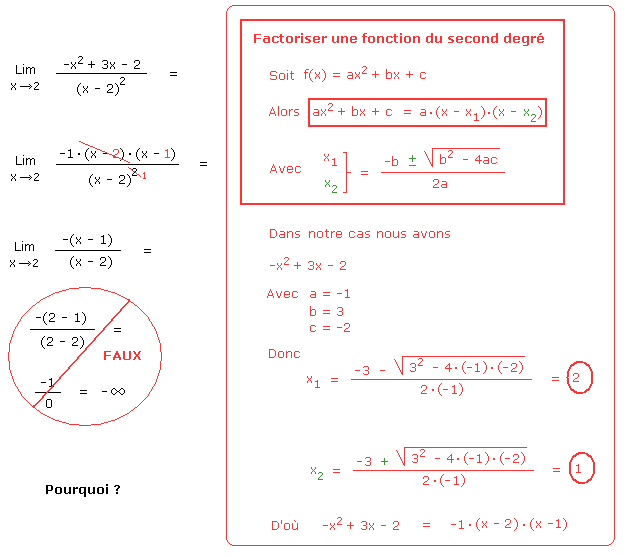
La solution proposée est fausse parce que si x tend vers 2 en venant de la droite, c'est-à-dire si x = 2,000001, alors la limite vaut -infini. Par contre si x tend vers 2 en venant de la gauche, c'est-à-dire si x = 1,999999, alors la limite vaut +infini.
Nous devons donc faire un tableau de signe.
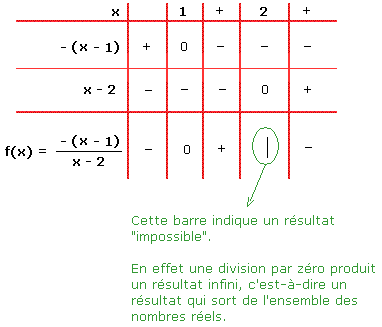
Ce tableau de signe nous permet de constater que la fonction sort de l'ensemble des nombres réels en x = 2. Cette sortie de l'ensemble des réels est provoquée suite à la division du numérateur par zéro. Il n'y a donc pas de solution possible en x = 2 puisque le résultat est infini. Plus précisément encore, nous savons, grâce au tableau de signe, que la fonction est positive à gauche de x = 2 et négative à droite de x = 2. Ceci nous permet de conclure que si un petit bonhomme se balade sur la courbe et s'approche de x = 2 en venant de la droite, et bien il sera précipité dans une chute vers le bas à proximité de 2. Tandis que s'il s'approche de 2 en venant de la gauche, le petit bonhomme s'envole brutalement vers les cieux à l'infini à proximité de 2.
En language mathématique ceci se traduit comme suit:
Limite droite = Limite gauche = |
Visualisez graphiquement ce que nous venons de calculer :
On voit très clairement sur ce graphique qu'il existe une asymptote verticale en x = 2. En calculant la limite gauche et la limite droite, nous venons en réalité de confirmer l'existence d'une asymptote verticale d'équation x = 2.
Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur privé en ligne vous aide en Math ou en Physique! Inscrivez-vous !