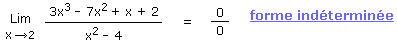Accueil > Limites : Théorie et Exemples > Exercices résolus > Solution 1.15


Limite : Factorisation du numérateur avec la Règle d'Horner
Solution de l'exercice 1.15

Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur privé en ligne vous aide en Math ou en Physique! Inscrivez-vous !



résoudre une forme indéterminée lors du calcul d'une limite

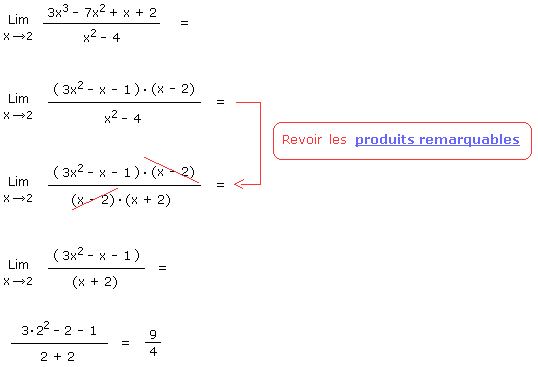
Ce cas indéterminé pourrait se résoudre par la règle de l'Hospital. Cependant je vous propose d'utiliser plutôt la Règle d'Horner pour factoriser le polynôme du troisième degré au numérateur. Nous pourrons ainsi simplifier la fraction et lever l'indétermination.

Comment utiliser la Règle d'Horner ?

La règle d'Horner est une technique facile pour diviser un polynôme par un diviseur tel que (x - a), a appartenant aux nombres réels.

Nous appellerons le résultat de cette division le quotient Q.

Et le reste de la division sera en général zéro puisque notre objectif est de réaliser une division sans reste afin de pouvoir factoriser notre polynôme.

Assez de blabla, voyez ci-dessous comment tout cela fonctionne :

I   Trouver a :

division de polynômes, principes de base

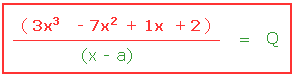
La grosse difficulté dans la factorisation de polynômes est de trouver la valeur de a. En réalité ce n'est pas si difficile que cela si l'on suit la méthode ci-dessous.

1) Identifier le terme indépendant :
a sera toujours un diviseur du terme indépendant. Le terme indépendant d'un polynôme est le terme qui n'est pas multiplié par un x. Dans notre cas, le terme indépendant du polynome 3x3 - 7x2 + x + 2 est 2.

2) Déterminer tous les diviseurs du terme indépendant :
2 peut être divisé par 1, -1, 2, ou -2.

3) Sélectionner la valeur qui annule le polynôme :
En effet, si on choisit a = 2 alors le polynôme 3x3 - 7x2 + x + 2 =
3 * 23 - 7 * 22 + 2 + 2 = 0.

4) (x - a) :
Notre diviseur (x - a) sera donc (x - 2).

II   Division du polynôme par Horner :

division de polynômes par Horner

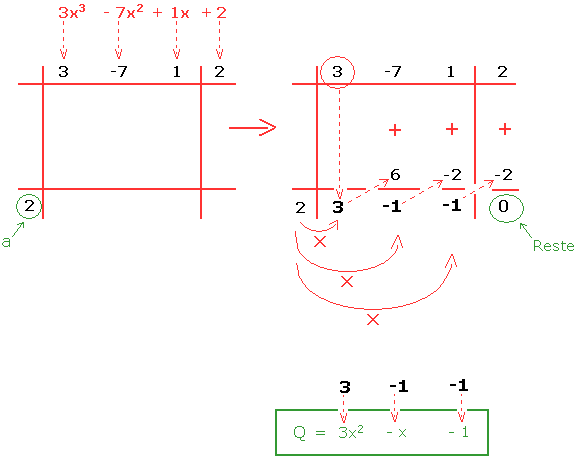
Tous les coefficients du polynôme doivent apparaître dans la première rangée du tableau dans l'ordre. C'est-à-dire d'abord le coeffcient du x3, puis celui du x2, ensuite celui du x et enfin le terme indépendant 2.

Le a (il vaut également 2 mais c'est une pure coincidence) se retrouve toujours en bas à gauche.

Si vous avez tout fait correctement, le reste doit toujours valoir zéro.

A la fin, les coefficients qui apparaissent dans la dernière rangée sont les coefficients du quotient Q. Le quotient Q aura toujours un degré égale au degré du polynôme d'origine moins un. En clair, cela veut dire que si le polynome est du 3ème degré, alors Q sera du 2ème degré (3 - 1 = 2). Donc dans l'ordre 3 sera le coefficient du x2, -1 sera le coefficient du x et -1 le terme indépendant de Q.

III   Factorisation du polynôme :

factoriser un polynôme avec Horner

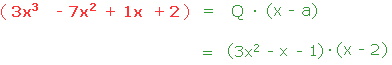
Nous avons finalement factorisé ce numérateur. Nous pouvons à présent simplifier la fraction et l'indétermination de la limite aura été levée.

Factoriser un polynôme avec les identités remarquables et la règle d'Horner

Et pour terminer, regardons le graphique de cette fonction :

Calculatrice scientifique online pour tracer de la fonction f(x) = (3*x^3-7*x^2+x+2)/(x^2-4)

Voyez comment la fonction comporte un trou (ou un saut) en x = 2. En effet, la courbe est discontinue et la fonction ne comporte pas de valeur y pour x = 2. Pourtant à proximité de x = 2 on peut voir que y se rapproche de 9/4, soit de 2,25. Ce graphique montre donc bien que si x tend vers 2 alors f(x) (ou y) tend vers 9/4 (= 2,25).


Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur privé en ligne vous aide en Math ou en Physique! Inscrivez-vous !



← Limite de fonction