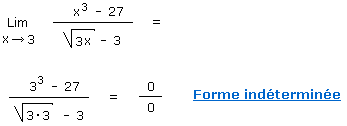Limite : Utiliser le binôme puis le trinôme conjugué
Solution de l'exercice 1.17

Avant d'attaquer la résolution de cet exercice et de lever la forme indéterminée obtenue, consultez les produits remarquables du binôme conjugué ainsi que du trinôme conjugué.

Vous pouvez également consulter les 3 exercices suivants qui utilisent justement le binôme et le trinôme conjugué : exercice 1.4, exercice 1.10, exercice 1.11.

Pour résoudre le cas d'indétermination suivant, nous allons multiplier le numérateur et le dénominateur par le binôme conjugué du dénominateur. Ensuite nous remplacerons le numérateur par son produit remarquable, en utilisant le trinôme conjugué.

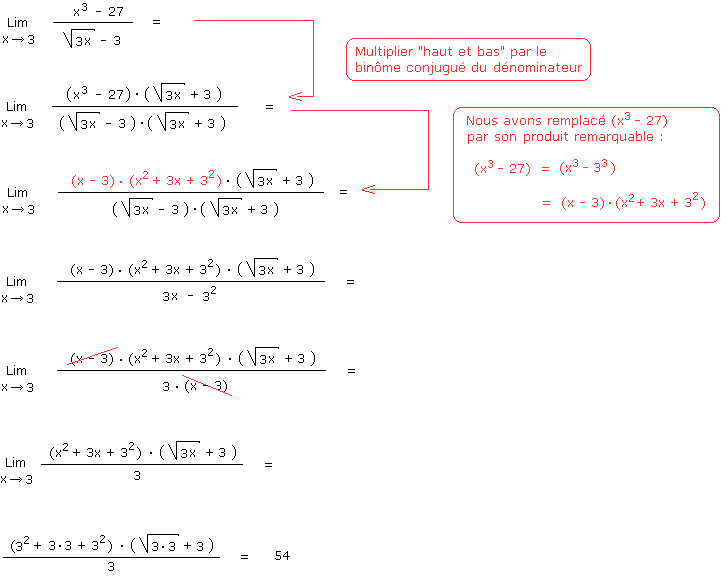
Observons un instant le graphique de cette fonction :

Remarquez le saut (trou) en x = 3. La fonction n'étant pas définie pour x = 3 (c'est-à-dire que x = 3 est hors du domaine de définition de cette fonction), la courbe ne contient pas de point à cet endroit. Cependant si l'on se rapproche de x = 3, alors y se rapproche de 54. C'est pourquoi nous pouvons dire que la limite de la fonction pour x tendant vers 3 vaut 54.

Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.