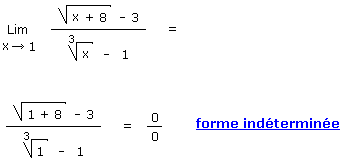
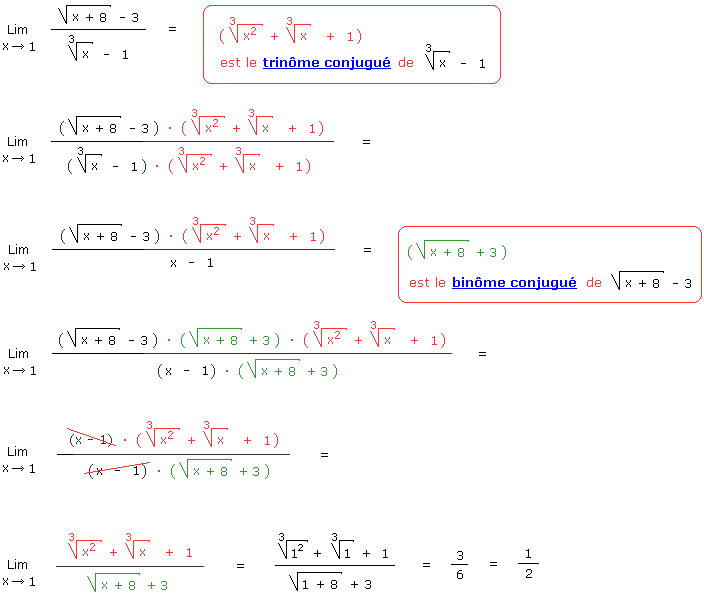Limite : Résoudre sans utiliser l'Hospital I
Solution de l'exercice 1.18

Avant d'attaquer la résolution de cet exercice et de lever la forme indéterminée obtenue, consultez les produits remarquables du binôme conjugué ainsi que du trinôme conjugué.

Vous pouvez également consulter les 4 exercices suivants qui utilisent justement le binôme et le trinôme conjugué : exercice 1.4, exercice 1.10, exercice 1.11, exercice 1.17.

Observons un instant le graphique de cette fonction :

Si vous rapprochez vos yeux de l'écran, vous verrez qu'il y a une discontinuité sur la courbe en x = 1. Cela est du au fait que la fonction n'est pas définie pour cette valeur de x. En d'autres mots 1 sort du domaine de f. Néanmoins la valeur de la limite existe et ainsi pour x tend vers 1 la limite de f vaut 1/2.

Vous souhaitez obtenir de l'aide pour résoudre un exercice ou un problème de math ? Posez toutes vos questions sur notre forum de math.