Limite d'une valeur absolue |x|
Solution de l'exercice 1.12
Vous recherchez un professeur particulier compétent et pédagogue ?
Nous vous proposons des cours particuliers à domicile pour vous aider en Math ou en Physique. Demandez plus de renseignements...
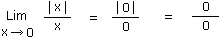
Nous obtenons le cas indéterminé 0/0.
Remarque importante : ici nous ne pouvons pas utiliser la règle de l'Hôpital car |x| n'est pas dérivable autour de 0. En effet la fonction f(x) = |x| présente une pointe, ou encore un angle en x = 0 (cliquez ici pour visualiser la courbe f(x) = |x|). C'est-à-dire que la pente de la fonction |x| passe brutalement d'une pente négative à une pente positive au point x = 0. Toute fonction qui présente cette caractéristique en un point (ici en x = 0) n'est pas dérivable en ce point.
Par contre on peut commencer par faire un tableau de signe pour étudier sur quelles valeurs de x la fonction est successivement positive et négative.

Dans ce tableau, la barre verticale indique qu'il n'existe pas de valeur en x = 0. En effet, zéro est hors du domaine de définition de cette fonction puisque 0 ne peut jamais se retrouver au dénominateur d'une fraction. De plus ce tableau nous permet de savoir que pour x < 0, le signe de la fonction |x|/x est négatif. Tandis que pour x > 0, le signe de la fonction |x|/x est positif.
Cette information est d'une importance capitale. En effet, cela veut dire que la limite de |x|/x pour x tend vers 0 est différente si vous vous approchez de x = 0 en venant par la droite ou en venant par la gauche. Assez de blabla, calculons cette limite ...
Limite gauche : 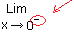
Calcul de la limite en venant de la gauche, c'est-à-dire qu'on s'approche de x = 0 en venant des x négatifs :
Limite droite : 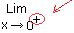
Calcul de la limite en venant de la droite, c'est-à-dire qu'on s'approche de x = 0 en venant des x positifs :
La limite gauche = -1 tandis que la limite droite = 1. Lorsque la limite gauche et la limite droite ne sont pas égales, on dit que la limite n'existe pas. Par contre il existe bien une limite gauche et une limite droite. |
Observons à présent le graphique de la fonction f(x) = |x|/x :
On voit très bien sur ce graphique que la fonction à pour valeur -1 partout à gauche de l'axe des x et +1 partout à droite de l'axe des x. Par contre, en x = 0, la fonction présente un saut. C'est-à-dire qu'il n'existe pas de valeur de y pour x = 0. Et il n'y a donc pas de point sur la courbe en x = 0.
Cependant, si l'on se positionne un tout petit peu a gauche de l'axe des x, la fonction vaut -1. C'est la valeur de la limite gauche que nous sommes entrain de vérifier graphiquement. Et si l'on se met un tout petit peu à droite de l'axe des x, la fonction vaut +1. C'est la valeur de la limite droite que nous venons de vérifier sur le graphique.
Vous recherchez un prof particulier compétent et pédagogue ?
Un professeur privé à domicile vous aide en Math ou en Physique! Inscrivez-vous !

